TEMA 7: TEORÍA DE LA PROBABILIDAD

La probabilidad es una causa de la certidumbre asociada a un suceso o evento futuro y suele expresarse como un número entre 0 y 1 (o entre 0 % y 100 %).

Una forma tradicional de estimar algunas probabilidades sería obtener la frecuencia de un acontecimiento determinado mediante la realización de experimentos aleatorios, de los que se conocen todos los resultados posibles, bajo condiciones suficientemente estables. Un suceso puede ser improbable (con probabilidad cercana a 0), probable (probabilidad intermedia) o seguro (con probabilidad uno).

Posee tres vertientes:

PROBABILIDAD SUBJETIVA O PERSONALÍSTICA

La probabilidad mide la confianza que el individuo tiene sobre la certeza de una proposición determinada.

 Por ejemplo: los epidemiólogos se basan en la experiencia para afirmar que el próximo invierno la epidemia de gripe tendrá una probabilidad del 0,0018 (180 casos por 100.000 habitantes).

 Este concepto de las probabilidades ha dado lugar al enfoque de análisis de datos estadísticos llamado “Estadística Bayesiana”.

PROBABILIDAD CLÁSICA O “A PRIORI”

desarrollada para resolver problemas relacionados con los juegos de azar (dados, monedas, ruletas…) 

Las probabilidades se calculan con un razonamiento abstracto. 

Ejemplo: no hay que lanzar el dado para saber que la probabilidad “a priori” de que salga el 6 es de 1/6=0,16.

LEY DE LOS GRANDES NÚMEROS

La probabilidad a priori de que salga un número en el dado es P(A) = 1/6 = 0,166 = 16,6 % Inicialmente esa probabilidad real puede no cumplirse pero si repetimos muchas veces el experimento, la frecuencia relativa de un suceso A, cualquiera, tiende a estabilizarse en torno al valor “a priori”

PROBABILIDAD RELATIVA O “A POSTERIORI” 

Un ejemplo:

SUCESOS:

• Sucesos independientes: Lanzar dos dados, tener 20 años y los ojos azules
• Sucesos dependientes: Ej. Extraer dos cartas de una baraja sin reposición, por ejemplo ser mujer y sufrir cáncer de mama 
• Sucesos compatibles: tienen algún suceso elemental común. Ej. A=obtener una puntuación par; B=obtener múltiplo de 3 
• Sucesos incompatibles o excluyentes: ningún suceso elemental común (A y B son contrarios). Eje. A=obtener par y B= obtener impar, A= hombre y B=mujer
• Unión de sucesos: es el suceso formado por todos los elementos de A y de B 

Reglas básicas: Teoría de la Probabilidad

Las probabilidades de un evento o suceso siempre oscilan entre 0 y 1 

• La probabilidad de que un evento o suceso sea seguro es = a 1.

 • La probabilidad de un suceso o evento imposible es = 0

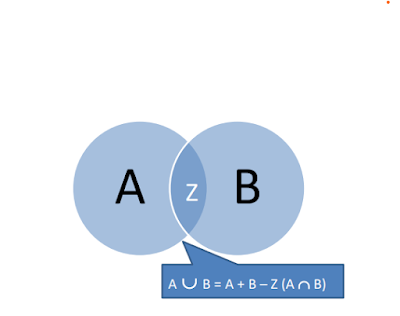
 • La unión de A y B es: – P(AUB)=P(A)+P(B)-P(A П B)

 • La probabilidad de un suceso contrario o del complemento es igual a 1 menos la probabilidad del suceso – P (A´)= 1-P(A)

 • La probabilidad de que ocurra el suceso A si ha ocurrido el suceso B se denomina probabilidad condicionada I y se define:

Teorema de Bayes

Expresa la probabilidad condicional de un evento aleatorio A dado B en términos de la distribución de probabilidad condicional del evento B dado A y la distribución de probabilidad marginal de sólo A. En términos más generales el teorema de Bayes que vincula la probabilidad de A dado B con la probabilidad de B dado A. Por ejemplo, sabiendo la probabilidad de tener un dolor de cabeza dado que se tiene gripe, se podría saber (si se tiene algún dato más), la probabilidad de tener gripe si se tiene un dolor de cabeza.

Distribución de probabilidad en variables discretas:

1. binominal:

La distribución binomial es un modelo matemático de distribución teórica de (la normal es con variables continuas) variables discretas

 – Cuando se producen situaciones en las que sólo existen dos posibilidades (cara/cruz; sano/enfermo…)

 – El resultado obtenido en cada prueba es independiente de los resultados obtenidos anteriormente. 

– La probabilidad del suceso A es constante, la representamos por p, y no varía de una prueba a otra. La probabilidad de `A es 1- p y la representamos por p . 

– El experimento consta de un número n de pruebas.

Mediante esta distribución se resuelven los problemas que plantean:

 – Si al hacer un experimento hay una probabilidad p de que ocurra un suceso ¿Cuál es la probabilidad de que en N experimentos el suceso ocurra X veces?

 • P: probabilidad de ocurrencia; p de no ocurrencia 

• X: numero sucesos favorables

• N: numero total de ensayos

2.Distribución de Poisson:

Poisson: médico miliar francés que estudia en el s.XIX la probabilidad de que un soldado muera en el campo de batalla por golpes de un caballo (También se llama la distribución de probabilidad de casos raros)